The program offers you the possibility to insert a preset text in a special section of the Office or in other programs.
And all this with a single Windows keyboard shortcut. This saves a lot of time.
At first glance, QuickTextPaste looks pretty easy to insert with just a text box for entering text with the hotkey. However, there are more functions here, such as running programs, opening web pages, pasting images from the clipboard, and pasting clipboard data as HTML
At first glance, QuickTextPaste looks pretty easy to insert with just a text box for entering text with the hotkey. However, there are more functions here, such as running programs, opening web pages, pasting images from the clipboard, and pasting clipboard data as HTML
Inserting plain text
includes a number of additional variables, such as date and time, when you want to use date and time variables.These powerful features dynamically complement static content such as date and time stamps, or wildcard placeholders, they can also launch programs or open documents that will be started by keyboard shortcuts.
It's easy to use! Some useful information on how to use and work:
► ... see the Quick-Text-Paste FAQ!
Here is an useful example, of the many helpful options or capabilities that you can do with Quick.Text.Paste with just a combination of keys, what you can do, for faster and more efficient work, ergo more free time for the important things in life: ► Send pictures via file path to a program via the clipboard!
| (Image-1) Paste images via image path to an active program via windows clipboard! |
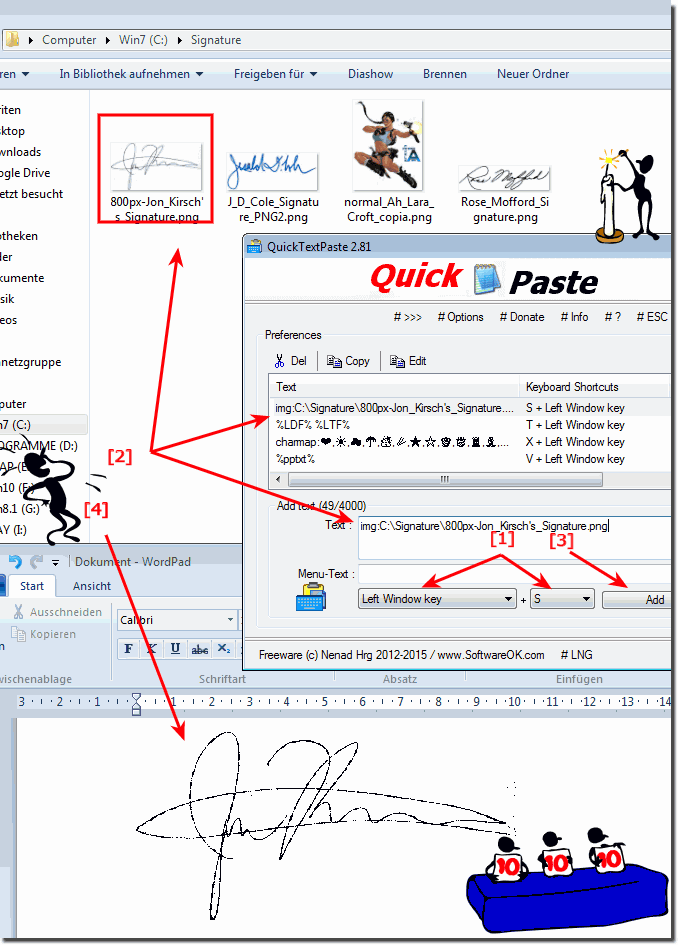 |
Everyone has situations in which it is often necessary to insert a certain text, a sentence, images, and date into the document just to be entered. Of course you can do all these commands with a computer mouse, or hot keys on the keyboard. But it is faster and more convenient to use special such a small program created for such tasks and situations.
