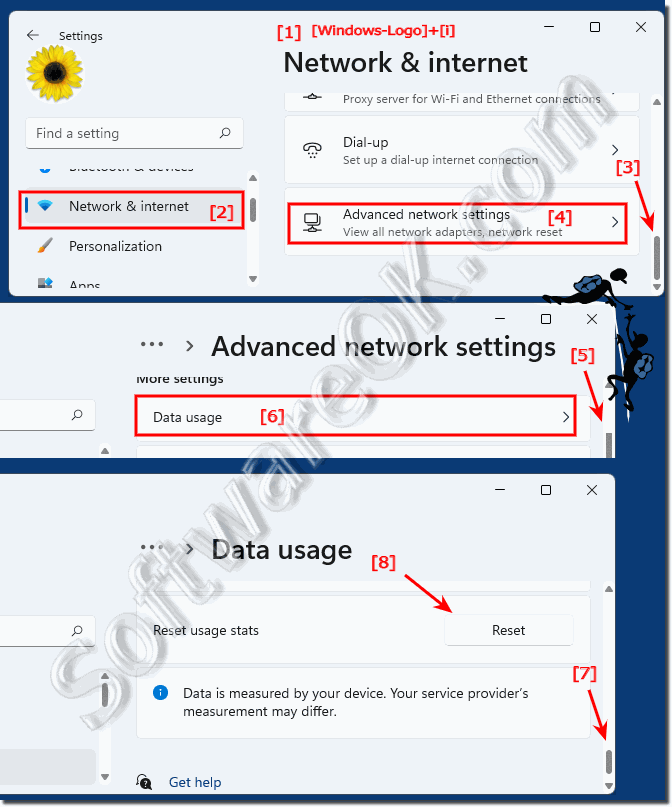
In Windows 11 you can set an internet data limit so that your PC does not use more than the allowed amount of data!The nice thing is that in Windows 11 you can set an individual data limit for each Wi-Fi network. You can also set a limit for an Ethernet connection. 1.) ... Setting the Internet data limit on Windows 11!
|
| (Image-1) Set internet data limit in Windows 11! |
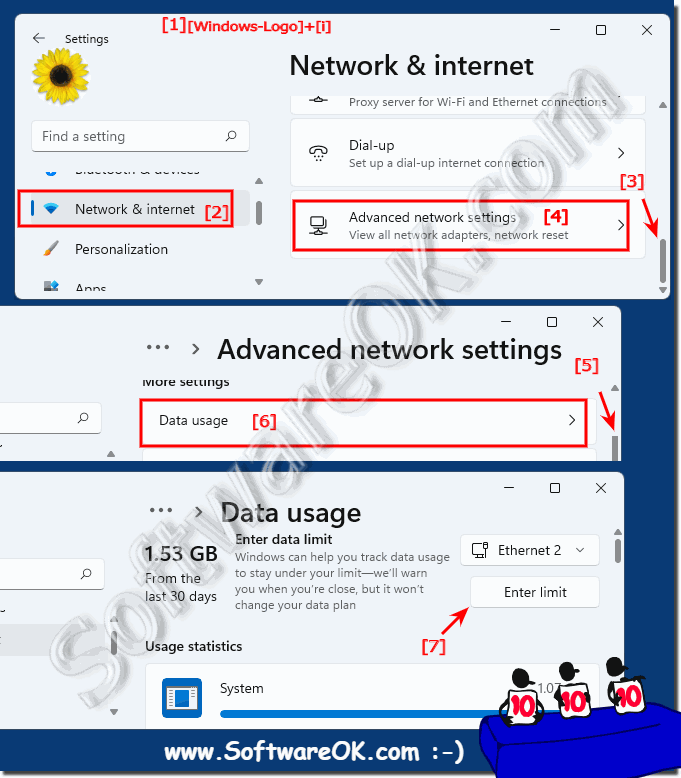 |
2.) ... Remove a network data restriction under Windows 11!
To remove the data restrictions from your PC, you can remove the data cap. To do this, open the Windows settings and navigate on your PC to Network & Internet> Advanced network settings> Data usage.
As described above: ► Setting the Internet data limit on Windows 11!
As described above: ► Setting the Internet data limit on Windows 11!
On the "Data Usage" screen in the upper right corner, click "Remove Limit" or "Edit Limit"
| (Image-2) Edit or remove Internet data limit in Windows 11! |
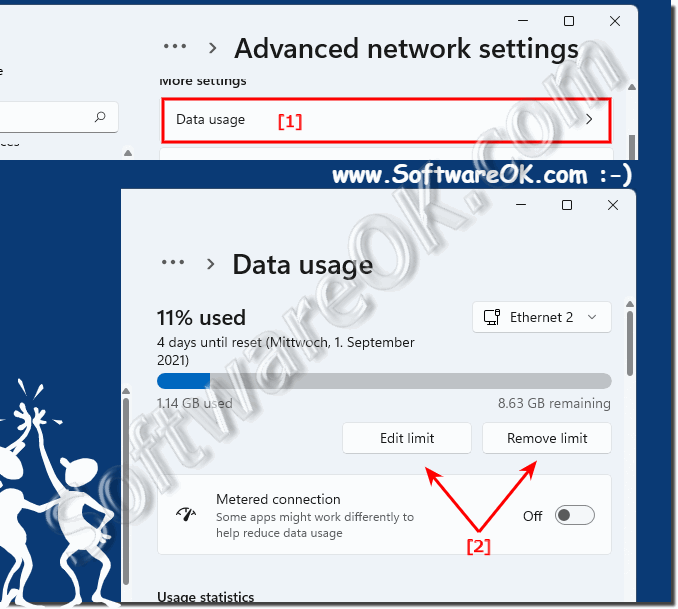 |
3.) ... reset data usage statistics in Windows 11!
1. Start the Windows 11 settings ( Windows + i )
2. Go to ► Network and Internet ,
3. Scroll on the right-hand side to ► Advanced network settings
4. Scroll on the right-hand side again to ► Data usage
5. Scroll on the right to ► Reset usage stats
(... see Image-3 Point 1 to 8)
4.) Why the restriction of Internet data usage!
You can use this function if, for example, you have a cellular connection or if your internet plan offers only limited data. With this method, you will know when you have reached your allowable data limit.And that's all you need to set a data limit in Windows 11. When you are approaching your data limit, you will receive a warning from your PC. You can then either continue to use the Internet or stop using it.
5.) More information about Internet and network under Windows 11!
► Windows 11 Network Tips
Under Windows 11 and Windows 10 there are two main components for the internet and network: network adapter, network driver.
You can share files and folders on your PC with other PCs and devices on the network. For example, you can share documents or photos with others.
► See WLAN or WiFi speed under Windows 10/11!
If you have problems with your internet or network:
► Identify network problems using the command prompt!
► The network drive folder keeps disappearing?
To share files and folders on your PC with other PCs and devices on the network, you need to enable file sharing. You can turn on file sharing in the Settings app under Network & Internet.
► Simply share the folder with everyone under Windows 11!
► For network adapters, a shortcut on the Windows 11, 10, ... desktop!
FAQ 121: Updated on: 23 April 2024 07:40