How long has my Windows 8.1 or 10 PC been running?
To see how long has the MS OS Windows 10 or 8.1 Computer been running, the solution is simple, or to see last restart time or Install-Date!
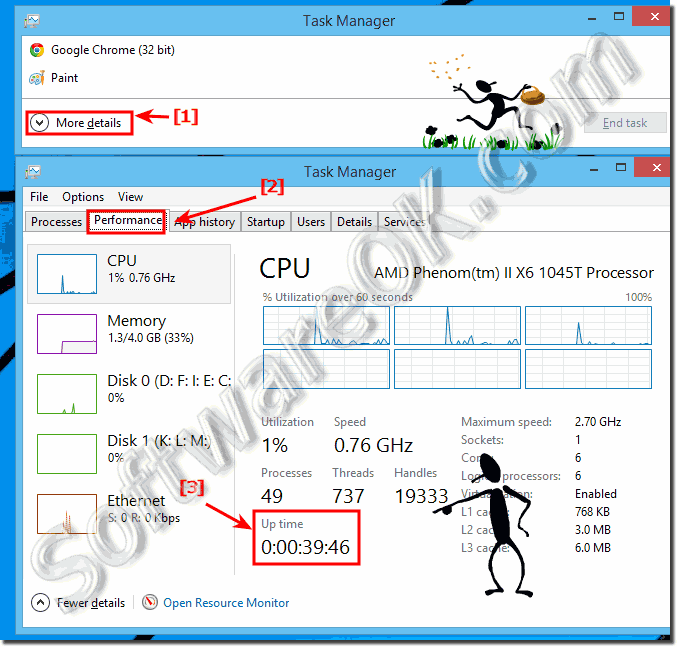
1. Open Windows Task Manager 8.1 Shortcuts [Windows Logo] + [SHIFT] + [ESC]
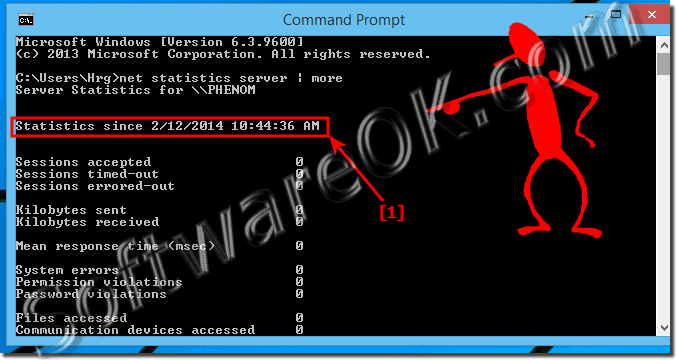
Start the Windows 8.1 / 8 command prompt and enter the command net statistics server | more
(Image-1) Statistics using the NET in Windows 8.1!
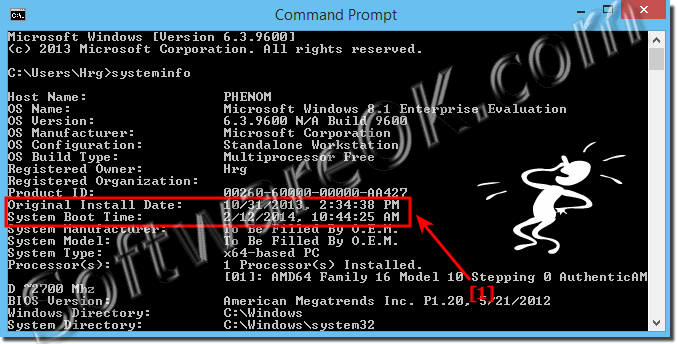
SystemInfo command!
(Image-1) System start (boot) time, Install-Date Windows!
Windows 10 Support END / October 2025
Windows 8.1FAQ 186: Updated on: 4 June 2022 14:11
Windows
If the navigation pane in MS Explorer was accidentally disabled in the Windows Explorer 8.1, the directory structure can be quite easy to become visible
To control aggressive programs and processes under Windows 8.1 and 10, the easy solution Content: 1. Check the performance and prioritization of processes
Here are some ways to find and Start the Windows 8.1 / 10 Task Manager, or create a Desktop Shortcut for the taskmgr.exe and Pin on Windows Start Menu Solutions
A Desktop shortcut, to start the Task Manager in minimized or normal window mode, the solution is simple and for all Windows 10, 8.1, 7, ie 11 The solution
If you want start the Google chrome browser to run on Windows 8.1 or 10 in the Metro APP mode or switch from Metro to desktop mode, the solution is very
Sometimes you want fast to dock two directories, or documents, and compare, here is the solution for Windows 7, 8 , 8.1 and Windows 10. Thanks to the docking
Here, the solution to go back to extra large icons in the thumbnail view of Windows 8 an 8.1 Content: 1. Switch Thumbnails over Windows Explorer View
»» My question is not there in the FAQ
Asked questions on this answer:
How to see for how much time the pc has been on in Windows 8.1 and Microsoft Windows 10?
Computer running time win 8.1 or Windows 10?
How to check how much time pc running in windows 10?
How can i tell how long my windows server 2012 has been up?
Find out how long Windows 8.1 has been running?
How long has windows 8 been out?
Command for checking how long windows pc is running?
Pc running times, how to find how long the the computer been running for Windows 8.1 and Microsoft Windows 10?
When has my computer been disconected?
How long Windows 8.1 computer or server has been running?
Command to know how long the computer has been running on windows server 2003?
How long has my Windows 8 system been up and running?
How to Check How Long my Windows Computer Has Been Up & Running?
How to know how long your pc has been running Windows 8.1 and Microsoft Windows 10?
What's a fast way to find out how long my Windows system has been running?
How long has windows 8 been out or how long wins 8.1 has been running?
How long the computer was on in Windows 8.1 and Microsoft Windows 10?
Can I find out how long I've been running my computer since I last boot of Windows?
Windows 8 has been around for how long?
How long since my Win 10 MS OS pc booted?
How to find runtime of pc in windows 8.1?
Windows 8.1 uptime, how long has win 8.1 been out?
Window 8.1 64 bit task manager?
How long since my computer's been on?
Check time server 2012 has been running?
How long is my computer running?
Win 8.1 check how long system been running?
Check to see how long windows 10 has been booted?
How to know how long my Windows 8.1 computer has been running?
How long's it been since last rebooted Windows 8.1?
How to tell how long a computer has been up Windows 8.1 and Microsoft Windows 10?
How long windows 10 computer has been on?
Measuring Windows 8.1 uptime, How long's?
Find how Long my Win 8.1 Computer Has Been Up and Running?
W 8.1 running time, how long the pc is on?
Find how long a server has been up 2012?
How to find out how long your computer has been on w 8.1 or Windows 10?
How to check uptime in Windows 8.1 and 10?
How to see running timer in Windows 8.1 and Microsoft Windows 10?
How long has windows 8.1 been out or windows 8 computer running since to track how long computer running software?
How long has windows 8.1 been out?
Lastbootuptime Windows 8.1 and Microsoft Windows 10?
How long has my pc been on check in windows 8.1 and Microsoft Windows 10?
Running since the last reboot od my Windows 8.1 and Microsoft Windows 10?
Keywords: windows, ten, 10, eight, 8.1, system, time, long, been, running, ms, os!, Questions, Answers, Software